Colaborando con nuestros compañeros de Airquitectura: Inteligencia Artificial aplicada a la Arquitectura hablábamos de la posibilidad de conocer las palancas que actúan en el precio de venta de un determinado activo para adecuarnos a ellas en la fase de proyecto. La pregunta es clave: ¿Qué debo potenciar en el proyecto para optimizar la rentabilidad?
Hay parámetros que sabemos, intuitivamente, que son claves. Superficie, orientación, altura… pero aplicando ciencia de datos, podemos obtener cosas muy curiosas… y datos muy concretos.
Datos de precios de activos inmobiliarios.
Como hemos visto en otros posts podemos analizar cientos de miles de datos de los cientos de miles de activos inmobiliarios que están publicados en las principales páginas de compra-venta inmobiliaria. Esos datos pueden ser calificados, ordenados, analizados. Y podemos operar con ellos.
Incluso si presuponemos que los anuncios que desaparecen y no vuelven a aparecer son activos que se han vendido/alquilado, teniendo una buena serie histórica también podremos analizar qué características tienen los activos con mayor demanda.
Pero, incluso solo con los activos en venta, seremos capaces de analizar muchos parámetros. Los precios de venta, aunque varíen finalmente en la compra, marcan una tendencia clara.
Regresión lineal.
Primero debemos conoce que es una regresión lineal. La regresión lineal es un modelo matemático usado para aproximar la relación de dependencia entre una variable dependiente -en nuestro caso el precio final-, una variable independiente -en nuestro caso, precio por metro cuadrado-, y un término aleatorio fijo o constante -en nuestro caso, precio mínimo-.
Este modelo puede ser expresado como Precio Final = Precio por metro cuadrado x metros cuadrados + precio mínimo.
Así, si descargo todos los precios y superficies de activos en venta de una determinada zona podré conocer esa ecuación matemática que me dirá la relación de dependencia.
Pongamos como ejemplo concreto de Regresión lineal.
Tenemos tres apartamentos de un dormitorios en la misma planta del mismo edificio. Son iguales, solo cambia la superficie. El apartamento A tiene 50 metros, el B tiene 60 y el C tiene 40.
El apartamento A, con 50 metros cuadrados, tiene un precio de venta de 150.000 euros. Podemos pensar que el precio es 3.000 euros por metro cuadrado… y es cierto. Pero un piso de similares características -pongamos el «B»- pero que tuviera 60 metros cuadrados, quizás no tendrá un precio de 180.000 euros. Quizás su precio sea de 160.000. Es lo más habitual.
Y el apartamento C, de 40 metros cuadrados no tendrá un precio de 120.000… quizás 140.000. Como vemos, no se cumple esa linealidad de los de 3.000 euros por metro cuadrado.
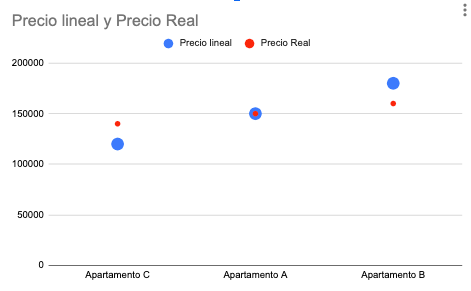
La regresión lineal me indica esa línea de precios, se la que sea… En este caso, la constante sería 100.000 euros, y la variable, 1.000 euros por metro cuadrado.
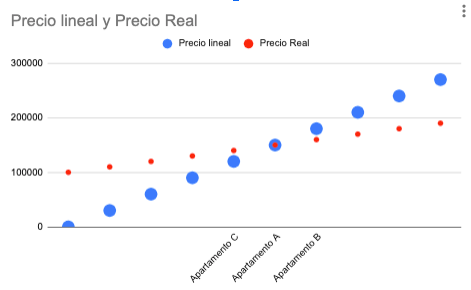
La fórmula matemática sería: Precio final = 100.000 + 1.000 x superficie. Si hubiéramos estimado Precio final = 3.000 x superficie, nos habría llevado a error.
Ajustando la línea.
No entraremos en detalles matemáticos. Pero parece lógico pensar que, cuando trabajamos con cientos de puntos, –¿estudiamos todos los activos en venta de una ciudad?– quizás una línea recta no sea lo que mejor se ajusta.
Podríamos entonces probar con ecuaciones logarítmicas, ecuaciones de segundo grado, potencias… No es excesivamente complejo, pero son de difícil visualización. Así que usaremos una software algo más especializado para su cálculo y representación. Nosotros usamos Tableau.
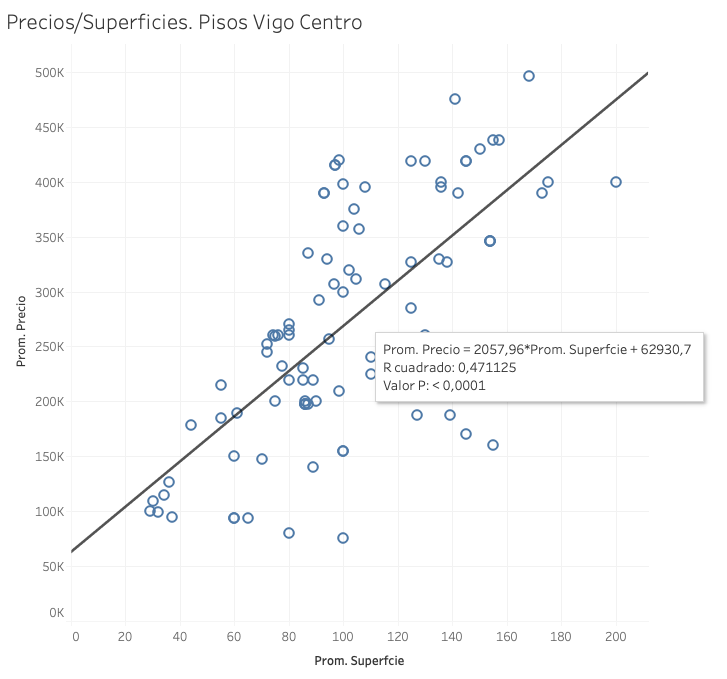
La ecuación lineal que explica los precios en Vigo-Centro, sería: Precio final = 62.930 euros + 2.056 euros x superficie.
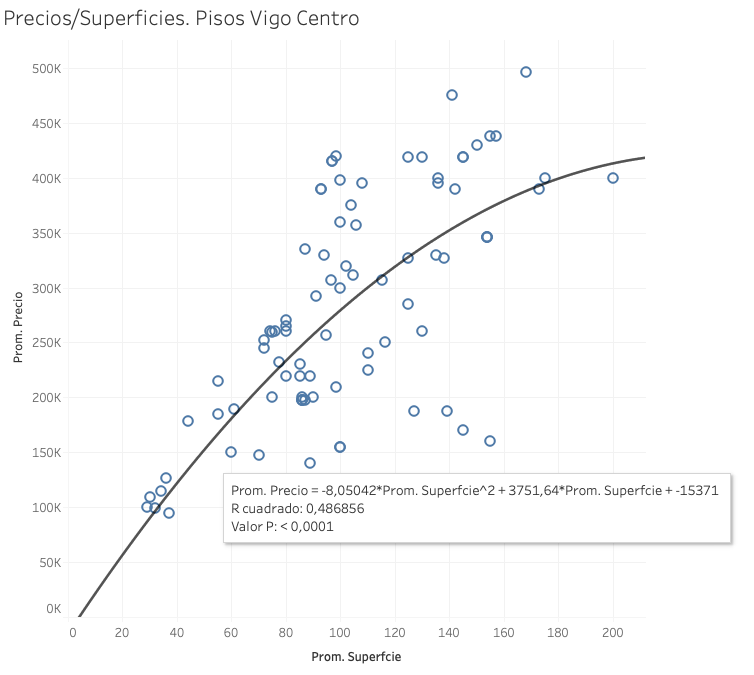
Pero observamos que la ecuación de segundo grado explica mejor la relación, pues tiene un Rcuadrado ligeramente superior. Así, la ecuación que explica mejor los precios en Vigo, zona centro, sería: Precio final = – 15.371 + 3.771 x superficie – 8 x superficie al cuadrado.
Una ecuación algo más compleja de visualizar mentalmente, pero muy sencilla con el software adecuado.
Modificamos parámetros en la Regresión Lineal.
Podemos estudiar la relación entre Precio y Superficie, pero también podemos modificar los parámetros. Por ejemplo, podríamos analizar la relación precio/numero de dormitorios. Veamos:
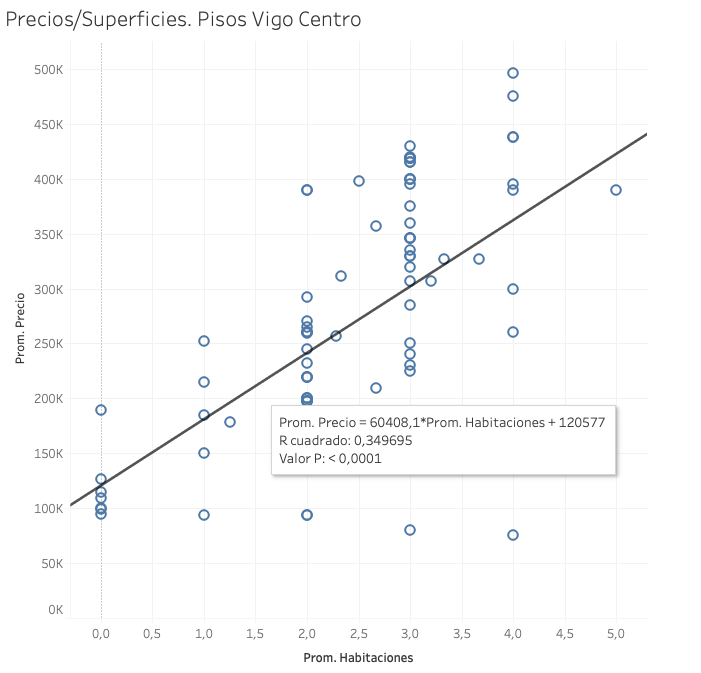
En este caso, la ecuación que explica el precio respecto al número de habitaciones, sería: Precio final = 120.577 euros + 60.408 euros x número de habitaciones. Aunque vemos que esta ecuación explica con menor exactitud que la que hacía referencia a la superficie –presenta un Rcuadrado inferior-.
Podremos analizar las ecuaciones según todos los datos que tengamos etiquetados en los activos: Superficie, habitaciones, número de baños, planta, garaje/trastero, API y tantas otras… y analizar cuál explica mejor el precio.
Aplicamos varios parámetros en la Regresión Lineal.
Finalmente podemos buscar una ecuación que incluya varios parámetros. Cuantos más datos y más parámetros relevantes, mayor será la exactitud.
Para realizar el cálculo necesitamos un software algo más potente. Nosotros usamos Python. Y resolvemos una ecuación que explica el «peso» que tienen cada uno de los parámetros en el precio de una vivienda.
Sería algo así: Precio Final = AxSuperficie + BxNúmero de Habitaciones + CxNúmero de Baños + DxTerraza/Balcón + ExPlanta + Fx(…)
Y con esa ecuación somos capaces de contestar a la pregunta que nuestros compañeros de Airquitectura nos hacían, para mejorar el desempeño de su software de Inteligencia Artificial aplicada a la Arquitectura…
